This is the first of two posts shared to introduce some of the background and theoretical ideas to consider regarding the transition to university mathematics, as well as provide an insight and links to some of the literature and scholarship in this area.
This post focuses on the transition and the specific problems and issues frequently noted for mathematics. The second post discusses some aspects/models of advanced mathematics at university which are particularly relevant to these issues.
University Transition
A successful transition is regarded as vitally important for both the overall success in the degree and for a successful learning experience. Much work on the transition to university concentrates on the issues of drop-out or retention. These issues may be the more prominent, visible indicators of difficulties with the transition, in the sense that they provide quantifiable easily observed phenomena (the student has left or is still on the course), but they do not tell the whole story. The recent national emphasis on the student experience focuses attention not just on preventing the student from dropping out, but also on ensuring that their experience is positive. Nonetheless, such research provides both models and clues about the issues that affect the transition. One of the messages from retention research is that there is rarely one sole cause for a student to drop-out [1], but rather a combination of contributory factors (Yorke & Longden, 2004). A student who does not drop-out may still be affected by many of these factors, and thus unhappy or having their learning seriously affected, but not to the level of dropping out [2].
Tinto’s (1975) theoretical work producing a conceptual schema of higher education drop-out is often used in the study of the transition to university (Figure 1). The schema, based on Durkheim’s theory of suicide, stresses the ‘social’ integration of the student in addition to the academic integration. Of particular importance for this project are the institutional, subject and educational commitments of the students, which along with their goals and motivations may be modified over time by their actual university experience and their interaction with the institution/faculty, ultimately affecting the success of the transition. In Tinto’s model, a lack of commitment leads to a lack of integration and these in turn affect success. Alternatively, a lack of integration can produce a lack of commitment (whether for academic, social or institutional purposes). These different commitments need not completely coincide, and a student who is still institutionally committed and socially integrated may, as a result of their academic experience and a lack of academic integration, lose their subject commitment, but continue with their degree.
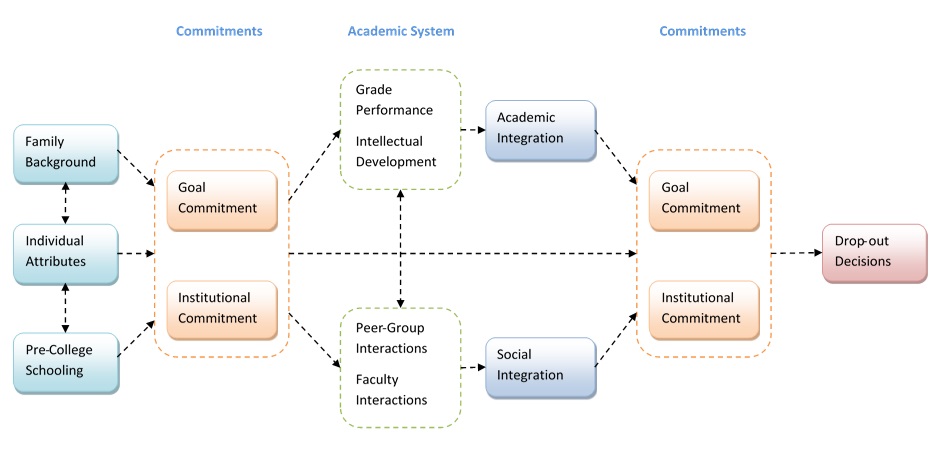
Notes:
[1] Drop-out due to one prominent cause unrelated to other factors does however happen, but is more often beyond the control of the university (sudden family tragedy or financial loss). This is not to say that universities cannot or do not try to help as far as is possible to accommodate such difficulties e.g. with support for time/year out.
[2] Indeed for some, it may be considered too late – they have committed to a course of study they are unhappy with but, for example, have neither the time nor money to start again. With the ever higher costs and sacrifices necessary for university education in the UK, this phenomenon could increase. In addition, there is the wish to avoid a very public failure or shame, despite deep unhappiness.
Trends
The mathematics education system has been affected by many government reports and changes over the last generation, some specific to mathematics, others more broadly focused on late secondary or university education. Reports include those by Dainton (1968), Cockroft (1982), Dearing (1985), DfE (1994), the Dearing (1997) report on HE, school curriculum changes in 2000 and 2004, a mathematics review by Smith (2004), and the 14-19 review by Tomlinson (2004). Over the last decade, one major focus has been on widening participation and recent government policy has been influenced by economic concern over the future supply of STEM graduates (Royal Society 2006, 2008). The expansion in participation is under threat from the recent recession and possible government cuts and may be influenced by the outcome of the current review into university funding.
The major preparation (in England and Wales) for a university mathematics degree has historically been the A-Level course and examination. However, the effective purpose of this examination has changed considerably since its inception in 1951 from a university set normatively-graded entrance examination, to a criteria-graded de-facto school leavers’ qualification, with little direct university involvement, to again, effectively a university entrance qualification, as increasing numbers have stayed beyond 16 and then increasingly to university (Hoyles, Newman, & Noss, 2001). Arguments surrounding the grading structure and standards as well as the syllabi are common. This changing purpose makes it unsurprising that mismatches in expectations and experience appear during the transition. In addition, those entering university are now from a much broader range of backgrounds, not just socially but educationally too. Indeed in this study not all of the students came through the traditional A-Level route.
Even within the route, the educational backgrounds have broadened. Whilst in 1965 38 per cent of A-Level pupils took only science subjects, by the 1990s the figure was only 9 per cent (DFEE data cited in LMS, 1995), and most mathematics undergraduates now enter university with only single, rather than double, mathematics A-Level and rarely with the cognitively supportive subject of physics as well. Changes to the school curriculum, such as Curriculum 2000, have lately concentrated on broadening the previously narrow spread of subjects studied, though at the natural expense of depth. Although the collapse in the study of further mathematics between the mid 1960s and mid 1990s (LMS, 1995) has started to recently reverse (Stripp 2004, QCA 2007), there is still a concern about the lack of mechanics preparation (Lee, Harrison, & Robertson, 2007) and there is a wide variety of topic combinations that can form the A-Level (LMS, 1995). The London Mathematical Society (LMS) (1995) criticised many of the changes as due to market effects and Hoyles, Newman and Noss (2001) similarly described trends as being due to external political and market pressures, rather than being led by learning and teaching based decisions. Such a heterogeneous educational base in a cohort makes it difficult for lecturers to accurately pitch their teaching and many will have only limited knowledge of the variety of curricula. The range of previous experience in the cohort can also affect the students as well, with those who have not for example studied further mathematics believing themselves to be at a disadvantage, even for topics which lecturers do not believe that this is the case [3] (Hoyles et al., 2001).
Notes
[3] This is an effect that I saw first-hand as an undergraduate. Friends without further maths lacked confidence on the topic of hyperbolic trigonometric functions even when we had studied considerably more at university than the rather basic introduction in the further mathematics syllabus.
Mathematics Transition
Cornelius’ (1972) study on the transition to university mathematics will seem familiar to many lecturers and students today; it is clear that many of the difficulties are either inherent in the general structure of our education system [4], or in the nature of advanced mathematics and the transition to this study.
Clark and Lovric (2008, 2009) propose a model based on the anthropological notion of a rite of passage, implications of which include the importance of social community, the “shock of the new”, transition as a process thus taking time, and the responsibilities of the student themselves. The students are part of a new academic community, studying a subject that differs in fundamental ways to their previous study, who in becoming part of that community need to develop a functional learner identity. Solomon (2007) notes a difficulty here as first year students struggle with a sense of “not belonging”, and not seeing themselves as “legitimate peripheral participants” (Lave & Wenger, 1991) who, whilst novices, can constructively engage with, and participate in, the subject.
One of the difficulties in attempting to match the two sides of the transition, secondary and tertiary education, in terms of experience and expectations (from both sides), is the problem of multiple purposes. The purposes the students have in studying mathematics, the purposes of the education systems, of examinations and indeed the purposes of mathematics itself may cover a range of options. It has been noted by many reports into the mathematics education system (Engineering Council 2000; LMS, 1992, 1995; Smith 2004) that mathematics has at least dual purpose to its study. For many, it is an important ‘service’ subject to the sciences, engineering, technology, medicine, and finance as well as everyday life. It is however in addition a theoretical academic subject in its own right and many wish to study mathematics itself rather than for external application. Such differences impact on students’ beliefs about the nature of the subject and their motivation for studying it. Some may have postgraduate study or research in mind, others may intend to utilise their advanced mathematics skills in a profession (e.g. teaching, finance). Some may go on to rather unrelated graduate careers. Such conflicting pressures were additional factors in creating the MMath degree (LMS, 1992).
Notes
[4] Student queries of why there are so many examination boards were made in this 1972 study and could be, and are, made today.
Beliefs
Differences in beliefs and motivations between students and lecturers due to this dual nature may create problematic false expectations on both sides. The outlook of academics will typically be concentrated around the views of the successful student wishing to undertake a research career, whereas the students increasingly have a more diverse range of motivations. The students’ beliefs about the subject may well be connected with their motivations, future intentions and past experience which as noted, are quite diverse. Daskalogianni and Simpson (2001) investigated and categorized the range of beliefs that sixth-form students held about mathematics. The three dominant “macro-beliefs” presented in their research were described as “systematic”, “exploratory” and “utilitarian”. These different viewpoints were found to interact and affect a range of “micro-beliefs” as shown in the Table 1 below.
|
MACRO-BELIEFS |
||||
|
Systematic |
Exploratory |
Utilitarian |
||
|
MICRO-BELIEFS |
Nature of mathematics | methodical, logical | problem-solving, linking things | tool for other subjects, applied in life |
| Focus of exercises | follow a series of steps | understand different ways of thinking | obtain correct exam answer | |
| Working in mathematics | exact answer, similar exercises | explore things, enjoy challenge | known algorithms, study techniques | |
| Didactical contract | dependence on notes and teacher | dependence on own abilities | dependence on teacher | |
Table 1 Summary of Daskalogianni and Simpson's (2001) categories for students' belief about mathematics
The “micro-belief” areas in the table link students’ overall focus with the way they actually engage in the mathematics and their beliefs about its nature. A diverse cohort is likely to present with diverse “macro-beliefs” which may then affect their actual approach to study. Crawford et al. (1994) also link the “how” mathematics is learnt with “what” the subject is about. In contrast to the model above, their categorisation of answers to the question “what do you think mathematics is?” is hierarchical with five categories divided into two major types of conceptions: “Fragmented” and “Cohesive”.
A similar categorisation (five categories in two types) was produced for the approach students took, split into those concentrating on “reproduction” and those seeking “understanding”[5]. They linked the “reproduction” approach with a “fragmented” conception of mathematics and a “cohesive” conception with the “understanding” approach. One of the main messages from these studies for a lecturer is that the prior beliefs and conceptions of their students may influence their approach to study. Consequently, learning about one’s students’ conceptions about mathematics could be a useful way of dealing with the diversity of the cohort (indeed, Crawford et al. (1998) went on to produce a survey based on their categorisations).
| Category | Representative quotation | |
|
Fragmented |
A. Maths is numbers, rules and formulae. | Maths is the study of numbers and the application of various methods of changing numbers. |
| B. Maths is numbers, rules and formulae which can be applied to solve problems. | Mathematics is the study of numbers and their applications in other subjects and the physical world. | |
|
Cohesive |
C. Maths is a complex logical system and way of thinking. | Mathematics is the study of logic. Numbers and symbols are used to study life in a systematic perspective and requires [sic] the mind to think in a logical and often precise manner. |
| D. Maths is a complex logical system which can be used to solve complex problems. | Maths in an abstract reasoning process which can be utilised to explore and solve problems. | |
| E. Maths is a complex logical system which can be used to solve complex problems and provide insights used for understanding the world. | Techniques for thinking about observable, physical phenomena in a quantitative way and also for thinking more abstractly with little or no relation to the directly observable universe. |
Table 2 Crawford’s (1994) categories for student’s beliefs on the nature of mathematics
Notes
[5] This distinction is similar to the common terms of surface and deep learning approaches respectively.
The “mathematics problem”
It is not new for teachers to express dissatisfaction with the abilities or performance of their students, with the oft made comments that things were better in the past. The quotation below is typical of comments in many mathematics departments today [6], despite the fact that it was written in 1978:
Three attitudes of present day undergraduates to study are...
an expectation to assimilate new ideas without mental effort;
a reluctance to devote time to study and to practice;
the lack of persistence necessary to tackle exercises of a non-trivial nature
(Walkden & Scott, 1980, p. 45)
Indeed similar criticism for mathematics can be found earlier (e.g. Thwaites, 1972, p.5). However, to accept the long history of such comments is not to dismiss all concerns, either long running ones or claims of substantial recent change, especially where evidence has been sought. Even if the complaints are not in fact new and the same problems were encountered in the past, these ‘problems’ may be indicators of genuine natural difficulties for students. Those that claim a more recent shift may point to a mismatch that has developed between secondary and tertiary education. Indeed, the now common four-year undergraduate MMath degree was created in part to tackle this issue (LMS, 1992).
A few years later, the LMS, the Royal Statistical Society (RSS) and the Institute of Mathematics and its Applications (IMA) felt the need to respond to further “unprecedented concern amongst mathematicians, scientists and engineers in higher education about the mathematical preparedness of new undergraduates” (LMS, 1995, p.3) as concentrated in three areas of technical, analytical and conceptual skills:
Students have “a serious lack of essential technical faculty”;
“a marked decline in...analytical powers when faced with simple two-step or multi-step problems”;
Students “no longer understand that mathematics is a precise discipline in which exact reliable calculation, logical exposition and proof play essential roles” (LMS, 1995, p. 3).
A later Engineering Council (2000) report set out a range of evidence to back up the claim that the issues, although by no means new, had grown worse in recent years. If a particular student, or indeed a particular cohort, is indeed underprepared in the above skill areas, then it will negatively impact on their transition as they struggle with a course and university system whose expected level of prerequisite skill does not match the reality. As the precise profile of the undergraduate population becomes more diverse, in terms of background, intentions and past experience and education, it may become more difficult to easily deal with these common problems for first year mathematics students. The mismatch between individuals and unchanged university expectations of them may also grow worse.
Notes
[6] Similar complaints might also be found in other departments of course.
The next (second) post looks at some of the key aspects of the nature of advanced (university level) mathematics including some of the theoretical models and the research regarding how students learn and the difficulties they may face.
References
Clark, M. & Lovric, M. (2008) Suggestion for a theoretical model for secondary-tertiary transitions in mathematics. Math. Educ. Res. J., 20 (2), 25-37.
Clark, M. & Lovric, M. (2009). Understanding secondary-tertiary transition in mathematics. International Journal of Mathematical Education in Science and Technology, 40 (6), 755-776
Cockroft, W. (1982). Mathematics Counts. Committee of Inquiry into the teaching of mathematics in schools. London: HMSO.
Cornelius, M. L. (1972). The Transition from School to University Mathematics. The Mathematical Gazette, 56(397), 207-218.
Crawford, K., Gordon, S., Nicholoas, J. & Prosser, M. (1994). Conceptions of Mathematics andhow it is learned: the perspectives of students entering university. Learning and Instruction, 4, 331-345.
Crawford, K., Gordon, S., Nicholoas, J. & Prosser, M. (1998). University mathematics students’ conceptions of mathematics. Studies in Higher Education, 23 (1), 87-94.
Dainton, F. S. (1968). Enquiry into the flow of candidates in science and technology into higher education. London: HMSO.
Daskalogianni, K., & Simpson, A. (2001). A categorisation of upper sixth-form students' beliefs about Mathematics. In Proceedings of the British Society for Research into Learning Mathematics (Vol. 21, pp. 13-18). Manchester Metropolitan University.
Dearing, R. (1985). Review of 16-19 qualifications. London: COI.
Dearing, R. (1997). National Committee of Inquiry into Higher Education (Dearing Report). Norwich: HMSO.
DfE. (1994). Science and Maths. London: DfE.
Engineering Council. (2000). Measuring the Mathematics Problem. Engineering Council. Retrieved January 17, 2009, from http://www.engc.org.uk/documents/Measuring_the_Maths_Problems.pdf.
Hoyles, C., Newman, K., & Noss, R. (2001). Changing patterns of transition from school to university mathematics. International Journal of Mathematical Education in Science and Technology, 32(6), 829. doi: 10.1080/00207390110067635.
Lave, J., & Wenger, E. (1991). Situated learning: Legitimate peripheral participation. Cambridge University Press.
Lee, S., Harrison, M. C., & Robinson, C. L. (2007). Recent changes in A-level Mathematics: is the availability and uptake of mechanics declining yet more? Teaching Mathematics Applications, 111-118.
London Mathematical Society. (1992). The Future for Honours Degree Courses in Mathematics and Statistics. London: The London Mathematical Society. Retrieved December 31, 2008, from http://www.lms.ac.uk/policy/Future_of_Hons_Degree_Courses.pdf.
London Mathematical Society. (1995). Tackling the Mathematics Problem. London Mathematical Society. Retrieved December 31, 2008, from http://www.lms.ac.uk/policy/tackling_maths_prob.pdf.
QCA. (2007). Evaluation of participation in GCE mathematics: Final report. QCA.
Royal Society. (2006). A degree of concern? UK first degrees in science, technology and mathematics. The Royal Society.
Royal Society. (2008). A higher degree of concern. The Royal Society.
Smith, A. (2004). Making Mathematics Count. Department for Education and Skills (DfES).
Solomon, Y. (2007). Not belonging? What makes a functional learner identity in undergraduate Mathematics? Studies in Higher Education, 32 (1), 79-96
Stripp, C. (2004). The changes to AS/A Level Further Mathematics for September 2004. MSOR Connections, 4(3), 15-16.
Tinto, V. (1975) Dropout from Higher Education: A Theoretical Synthesis of Recent Research, Review of Educational Research vol.45, pp.89-125.
Tomlinson, M. (2004). 14-19 Curriculum and Qualifications Reform: Final Report of the Working Group on 14-19 Reform. Working group on 14-19 reform.
Thwaites, B. (1972). SMP: The First Ten Years. London: Cambridge University Press.
Walkden, F., & Scott, M. R. (1980). Aspects of mathematical education. International Journal of Mathematical Education in Science and Technology, 11(1), 45. doi: 10.1080/0020739800110108.
Yorke, M., & Longden, B. (2004). Retention and Student Success in Higher Education. SHRE and Open University Press Imprint. Maidenhead: Open University Press.